BRWIKI

Welcom to brwiki

Material_test-data-processing

# 材料試験自動データ処理

鋼材の材料試験の自動化データ処理スクリプト．
実現できる機能は　降伏点，引張強度の算出．ヤング率，ポアソン比の算出．最後に，自動でグラフを出力，レポートとしてExcelに保存する．

Google colab　ソースコードsource_code

# 導入

最初はcsv生データから，必要なデータを読み取り，応力，縦ひずみ平均値と横ひずみ平均値を算出する．

ここでは，生データのひずみチャンネル配置によらず，コードで数値の[+，-]を用いて，縦ひずみや横ひずみの判定を行った．

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
from glob import glob
from google.colab import drive
import csv
import numpy as np
from openpyxl import load_workbook
import matplotlib.pyplot as plt
 
###google driveに接続する．ローカル実行の場合は消してください．
drive.mount('/content/drive')
%cd '/content/drive/MyDrive/Colab_Notebooks/material_test'
###

filenames = glob('*.csv')
print(filenames)
 
#for filename in filenames:
with open('材料試験_H300W_No.1_データリスト.csv',encoding="utf8",errors='ignore') as f:
  f_csv = csv.reader(f)
  next(f_csv)
  data = list(f_csv)
  a = np.array(data)
  load = a[1:,2]
  a = a[1:,:]         #文字列の次から
  x = range(np.shape(a)[0])
  y = len(data) - 1     #行数を数える
  case1 = np.empty([y,8],dtype = float)
 
#########################
for i in x:
  case1[i,0] = a[i,2]  #load
  case1[i,1] = a[i,3]  #disp
  if float(a[int(y/2),4]) > 0 :   #縦ひずみを判定する
    case1[i,2] = a[i,4]       #縦ひずみ1を定義する
    if float(a[int(y/2),5]) > 0 : #縦ひずみを判定する
      case1[i,3] = a[i,5]     #縦ひずみ2を定義する
      case1[i,4] = a[i,6]     #横ひずみ1を定義する
      case1[i,5] = a[i,7]     #横ひずみ2を定義する
    else :
      case1[i,4] = a[i,5]      #横ひずみ1を定義する
      case1[i,5] = a[i,7]    #横ひずみ2を定義する
      case1[i,3] = a[i,6]    #縦ひずみ2を定義する
  if i == y :
    break
  striantate = (case1[:,2]+case1[:,3])/2        #縦ひずみ平均値
  strianyoko = (case1[:,4]+case1[:,5])/2        #横ひずみ平均値
############################
#　エクセルシート（テンプレート）を読み込む
wb = load_workbook("template_mt.xlsx", data_only=True)  #エクセルシートを導入する
wb1 = wb.active           #シートを選択する

#################
 
A = wb1['F9'].value   #断面積を取得する
case1[:,6] = case1[:,0] *1000/ A     #応力の算出
 
#################

降伏点の算出方

標準材料試験に対して，ひずみが4000まで，基本降伏点を超えているため，降伏点の算出は： > ひずみが4000までの最大応力とする．

引張強度は応力の最大値を取得する．

1
2
3
4
5
6
7
8
sigma_y = 0
i = 0
while striantate[i] < 4000:
  sigma_y= max(sigma_y,case1[i,6])
  i = i+1
sigma_u = max(case1[:,6])
print('降伏点：',sigma_y)
print('引張強度：',sigma_u)

# 最小二乗法を用いたヤング率の求め

  • 実験の初期ノイズおよび，降伏点付近の塑性化の影響を排除するため，ヤング率の算出範囲は (\(0.2\sigma_y - 0.7\sigma_y\))となった．

最小二乗法を用いて，曲線の傾き(\(k_1\))は以下のように算出された:

\[\begin{array}{c}k_1 = \frac{n \sum_{i=1}^{n} x_{i} y_{i}-\sum_{i=1}^{n} x_{i} \sum_{i=1}^{n} y_{i}}{n \sum_{i=1}^{n} x_{i}^{2}-\left(\sum_{i=1}^{n} x_{i}\right)^{2}} \end{array} \]

コードで見やすいため，以下のように省略で表記する． \[k_1 = \frac {na1 - a21\times a22} {nb1 - a21^2}\]

なお，決定係数(\(R^2\))については，残差の二乗和を標本値の平均値 (\(\overline{y}\))からの偏差の二乗和で割ったものを1から引いた値であり,以下のような式で算出した．

\[R^{2} = 1-\frac{\sum_{i=1}^{N}\left(y_{i}-f_{i}\right)^{2}}{\sum_{j=1}^{N}\left(y_{j}-\bar{y}\right)^{2}}\]


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
i = 0; a1 = 0; a21 = 0; a22 = 0; k1 = 0; b1 = 0; n=0;pc = 0
for j in case1[:,6]:
  if j > 0.2*sigma_y and j < 0.7*sigma_y:
    a1 += (striantate[i] * case1[i,6])
    a21 += striantate[i]
    a22 += case1[i,6]
    b1 += striantate[i] ** 2
    pc += strianyoko[i]/striantate[i]
    n += 1
  i = i+1

k1 = (n*a1 - a21*a22)/(n*b1-a21**2)     #yong's modulus
b0 = a22/n - k1*a21/n            #intercept　切片
pc = -pc/n                   #Poisson coefficient ポアソン比
####### R決定係数の求め
i = 0; ssr = 0; sst = 0
ymean = a22/n
for j in case1[:,6]:
  if j > 0.2*sigma_y and j < 0.7*sigma_y:
    ssr += (case1[i,6] - (striantate[i]*k1+b0))**2
    sst += (case1[i,6] - ymean)**2
  i += 1
R2 = 1 - ssr/sst        #R2 Coefficient of determination，決定係数
######
print('ヤング率E = ',k1*10**6)
print('ポアソン比 = ',pc)
print('決定係数R^2 = ',R2)

# グラフの出力

matplotlibを用いてグラフの出力

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
##############
#グラフを書く
plt.plot(striantate,case1[:,6], label="stress-strain",color='black',linewidth=0.75)
plt.xlabel("Strain")
plt.ylabel("Stress [$N/mm^2$]")
plt.ylim(0, 500)
plt.xlim(0, 70000)
plt.grid(color="k", linestyle=":") # メッシュ背景を点線に設定する
plt.legend(loc=4,numpoints=1)            #凡例
plt.savefig('stress-strain.svg')    #svgとして保存
plt.show()
###############
### データを書き込む
最後に処理完了したデータを全部Excelテンプレートに書き込む．
wb1.cell(6,10,sigma_y)
wb1.cell(6,11,sigma_u)
wb1.cell(6,12,k1)
wb1.cell(6,13,pc)
for i in range(3,y) :
  for j in range(2,8) :
    wb1.cell(i,j,case1[i-3,j-2]) #シートにi行j列にデータを書き込む
wb.save("111.xlsx")     #保存する

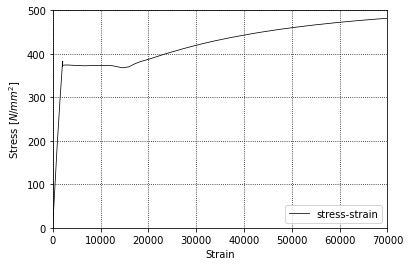
Full Code

  1. フォルダ内に.csvファイルを探して，名前を取得する．
  2. 生データを読み取り，データ処理を行う．
  3. 生データから，縦ひずみ，横ひずみ平均値と応力を算出する．
  4. 降伏点および引張強度を算出する．
  5. 最小二乗法を用いてヤング率およびポアソン比の算出．
  6. 応力－ひずみ関係グラフを書く，出力，保存する．
  7. 計算結果および生データをテンプレートに保存する．
material-test.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
from glob import glob
from google.colab import drive
import csv
import numpy as np
from openpyxl import load_workbook
import matplotlib.pyplot as plt
 
###
drive.mount('/content/drive')
%cd '/content/drive/MyDrive/Colab_Notebooks/material_test'
filenames = glob('*.csv')
###
m=1;  #生データ書き込むためcellの列数，
row1 = 6  #計算結果を書き込むための行数
############################
#　エクセルシート（テンプレート）を読み込む
wb = load_workbook("template_mt.xlsx", data_only=True)  #エクセルシートを導入する
wb1 = wb.active           #シートを選択する

######
for filename in filenames:
  fname = filename.split('_')[-2]
  with open(filename,encoding="utf8",errors='ignore') as f:
    f_csv = csv.reader(f)
    next(f_csv)
    data = list(f_csv)
    a = np.array(data)
    load = a[1:,2]
    a = a[1:,:]         #文字列の次から
    x = range(np.shape(a)[0])
    y = len(data) - 1     #行数を数える
    case1 = np.empty([y,8],dtype = float)
  
  #########################
  for i in x:
    case1[i,0] = a[i,2]  #load
    case1[i,1] = a[i,3]  #disp
    if float(a[int(y/2),4]) > 0 :   #縦ひずみを判定する
      case1[i,2] = a[i,4]       #縦ひずみ1を定義する
      if float(a[int(y/2),5]) > 0 : #縦ひずみを判定する
        case1[i,3] = a[i,5]     #縦ひずみ2を定義する
        case1[i,4] = a[i,6]     #横ひずみ1を定義する
        case1[i,5] = a[i,7]     #横ひずみ2を定義する
      else :
        case1[i,4] = a[i,5]      #横ひずみ1を定義する
        case1[i,5] = a[i,7]    #横ひずみ2を定義する
        case1[i,3] = a[i,6]    #縦ひずみ2を定義する
    if i == y :
      break
    striantate = (case1[:,2]+case1[:,3])/2        #縦ひずみ平均値
    strianyoko = (case1[:,4]+case1[:,5])/2        #横ひずみ平均値

  #################
  
  A = wb1.cell(row1,6).value   #断面積を取得する
  case1[:,6] = case1[:,0] *1000/ A     #応力の算出
  
  #################降伏点および引張強度の算出
  sigma_y = 0
  i = 0
  while striantate[i] < 4000:
    sigma_y= max(sigma_y,case1[i,6])
    i = i+1
  sigma_u = max(case1[:,6])
  ##############ヤング率の算出
  i = 0; a1 = 0; a21 = 0; a22 = 0; k1 = 0; b1 = 0; n=0;pc = 0;
  for j in case1[:,6]:
    if j > 0.2*sigma_y and j < 0.7*sigma_y:
      a1 += (striantate[i] * case1[i,6])
      a21 += striantate[i]
      a22 += case1[i,6]
      b1 += striantate[i] ** 2
      pc += strianyoko[i]/striantate[i]
      n += 1
    i = i+1

  k1 = (n*a1 - a21*a22)/(n*b1-a21**2)     #yong's modulus
  b0 = a22/n - k1*a21/n            #intercept　切片
  pc = -pc/n                   #Poisson coefficient ポアソン比
  ####### R決定係数の求め
  i = 0; ssr = 0; sst = 0
  ymean = a22/n
  for j in case1[:,6]:
    if j > 0.2*sigma_y and j < 0.7*sigma_y:
      ssr += (case1[i,6] - (striantate[i]*k1+b0))**2
      sst += (case1[i,6] - ymean)**2
    i += 1
  R2 = 1 - ssr/sst        #R2 Coefficient of determination，決定係数
  ##########グラフを書く
  plt.plot(striantate,case1[:,6], label="stress-strain",color='black',linewidth=0.75)
  plt.xlabel("Strain")
  plt.ylabel("Stress [$N/mm^2$]")
  plt.ylim(0, 500)
  plt.xlim(0, 70000)
  plt.grid(color="k", linestyle=":") # メッシュ背景を点線に設定する
  plt.legend(loc=4,numpoints=1)            #凡例
  plt.savefig(fname+'-stress-strain.svg')    #svgとして保存
  plt.show()
  ###############データの書き込む
  wb1.cell(row1,10,sigma_y)
  wb1.cell(row1,11,sigma_u)
  wb1.cell(row1,12,k1)
  wb1.cell(row1,13,pc)

  for i in range(15,y) :
    j1 = 0
    for j in range(m,m+6) :
      wb1.cell(i,j,case1[i-15,j1]) #シートにi行j列にデータを書き込む
      j1 +=1
  
  m += 6
  row1 += 1

  wb.save("test.xlsx")     #保存する

Matlab ver.

Matlabのバージョンも作っています．考え方は基本一緒．

material-test.m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
%%
clc                                 %コマンドウインドウをクリアする
clear                               %ワークスペースのクリア
file = dir(fullfile('*.csv'));      %csvファイルの情報を全部読み込む
filenames = {file.name};            %csvファイル名を取得
[~,n] = size(filenames);            %csvファイルの個数を数える
A = readmatrix('template_mt.xlsx','sheet',1,'range','F6:F8');   %断面積を取得する

%変数の定義
stressmax = 0; avx = 0; avy = 0; avx2 = 0;
Sxy = 0; Sx2 = 0; M = 0; Sxy1 = 0; Sxy2 = 0;

%%
%全てのデータを行列変換
%%%%figure
 figure1 =figure;
 axes1 = axes('Parent',figure1);
hold(axes1,'on');
ylabel({'Stress [N/mm^2]'});
xlabel({'Strain'});
%%%%%%%
for i = 1 : n
     stress_y(i) = 0;
    k = strcat(filenames(i));           %文字列に変換する
    data{i,1} = k{1,1};                 %名前を付けて
    data{i,2} = readmatrix(k{1,1});     %データを入れる
    f = data{i,2};                      %data中のi行2列のデータを取り出す
    f = f(:,3:8);                       %計測データの3～8列(荷重，変位，ひずみ*4)を取り出す
    data{i,2} = f;
    [j,~]=size(data{i,2});      %データ数の列数を数える
    if data{i,2}(j/2,4)>0          %縦ひずみ2を判定する
        next;
    else 
            data{i,2}(:,[4,5]) =data{i,2}(:,[5,4]);         %横ひずみと縦ひずみを並び替える
    end
    
    %応力・平均ひずみの出力
    for m=1:j
        stress(m) = data{i,2}(m,1)/A(i)*1000;           %`応力の出力
        strain(m,1) = 0.5*(data{i,2}(m,3) + data{i,2}(m,4));
        strain(m,2) = -0.5*(data{i,2}(m,5) + data{i,2}(m,6));
        if strain(m,1) < 4000
            stress_y(i)=max(stress(m),stress_y(i));
        end
    end
    stressmax(i) = max(stress);        %応力最大値を取得する

    %平均値を取得する
    for m=1:j
        if (stress(m) > (0.1*stress_y(i))) && (stress(m) < (0.7*stress_y(i)))
             avx = avx + strain(m,1);
             avy = avy + stress(m);
             avx2 = avx2 + strain(m,2);
             M = M+1;
        end
    end 
    avx = avx/M ; avy = avy/M; avx2 = avx2/M;
    %最小二乗法
    for m=1:j
        if (stress(m) > (0.1*stress_y(i))) && (stress(m) < (1.7*stress_y(i)))
            Sxy = Sxy+(strain(m,1)-avx)*(stress(m)-avy);
            Sx2 = Sx2+(strain(m,1)-avx)^2;
            Sxy1 = Sxy1+(strain(m,2)-avx2)*(strain(m,1)-avx);
            Sxy2 = Sxy2+(strain(m,2)-avx2)^2;
        end
    end 
    Yongs(i) = Sxy/Sx2*10^6;
    b = avy - Yongs * avx;
    Poissons(i) = Sxy2/Sxy1;
    
    plot(strain(:,1),stress);       %図の追加
end

writematrix(data{1,2},'template_mt.xlsx','sheet',1,'range','A15')
writematrix(data{2,2},'template_mt.xlsx','sheet',1,'range','G15')
writematrix(data{3,2},'template_mt.xlsx','sheet',1,'range','M15')
writematrix(stress_y','template_mt.xlsx','sheet',1,'range','J6')
writematrix(stressmax','template_mt.xlsx','sheet',1,'range','K6')
writematrix(Yongs','template_mt.xlsx','sheet',1,'range','L6')
writematrix(Poissons','template_mt.xlsx','sheet',1,'range','M6')

%%%Figure
xlim(axes1,[0 70000]);
ylim(axes1,[0 500]);
box(axes1,'on');
hold(axes1,'off');
legend1 = legend(axes1,'show');
legend('No.1','No.2','No.3','location','southeast');